Research Aims to Enable Data-Informed, Model-Based Predictions in Real-World Problems
Translating physical phenomena observed in nature – like weather and climate trends, hurricanes, or disease progression – into a mathematical framework may seem like a nearly impossible task, but Andreas Mang, assistant professor of mathematics at the University of Houston, is up for the challenge.

The National Science Foundation awarded him its most prestigious honor, the Faculty Early Career Development, or CAREER, award. The grant supports early-career faculty who can serve as role models in research and education. Mang received $499,997 for five years.
“I am excited, honored, and grateful,” he said. “I am thankful to my mentors, collaborators, and colleagues for their support and invaluable advice during my academic career. I am also thankful to my family, and particularly my wife, for their support and encouragement.”
Mang and his lab will work on inverse problems. This is a particular class of problems in which scientists try to infer unknown causes based on observations of their effects. For example, one seeks to identify the best parameters of a mathematical model (i.e., a mathematical abstraction of a physical phenomenon, such as disease progression), so that the model output (a computer simulation) best matches some observed data.
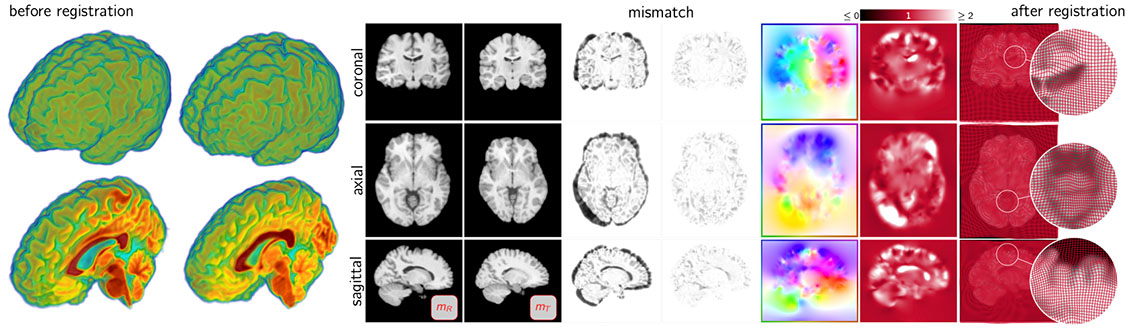
The ultimate aspiration of his group’s research is to use computer simulations to aid decision-making or enable model-based predictions. To make these predictions useful in practice, his group wants to be able to quantify the level of confidence they have in the generated predictions.
“My work will try to make these predictions accurately, efficiently, and rigorously for problems with billions of unknown parameters,” Mang said. “It will explore cutting-edge mathematical techniques to accomplish these goals.”
However, these calculations can create massive computational costs.
For example, Mang and his lab want to be able to tell a clinician how uncertainties propagate through computed predictions of tumor growth. Computing these confidence estimates and developing approaches to reduce uncertainties adds significant mathematical and computational challenges, resulting in intractable run times if suboptimal algorithms are considered.
To address these issues, his group will not only develop the methods to make predictions on physical phenomena, such as tumor growth, but they will do it in an efficient way. They will use dedicated hardware, like graphics processing units, and supercomputing platforms, for problems that have a lot of unknowns/model parameters.
Potential applications of his work include patient-specific simulation of the progression of a disease, climate modeling, weather predictions, and hurricane or tsunami predictions.
In addition to research development, Mang plans to create a new graduate course in the Department of Mathematics and an annual workshop to expose graduate students to cutting-edge research at the interface of applied mathematics and data-enabled sciences.
“They will learn about important topics related to inverse problems, optimal design, optimal control, and machine learning,” he said, “with a focus on applied and computational mathematics, scalable algorithms, and parallel scientific computing.”
He hopes these learning opportunities will help to expand the applied mathematics and computer science workforce and enable students to tackle modern societal challenges.
- Rebeca Trejo, College of Natural Sciences and Mathematics